近日，宁波大学张成杰教授课题组与中国科学技术大学量子信息重点实验室郭光灿院士团队合作在非厄密系统研究方面取得重要进展，利用量子光学平台在实验实现对非厄密算符不确定关系的研究。相关研究工作该成果以「Experimental Investigation of Uncertainty Relations for Non-Hermitian Operators （非厄米算符不确定关系的实验研究）」为题，于2024年2月15日在物理学领域权威期刊Physical Review Letters（物理评论快报）上发表。

星空在线,星空在线(中国)硕士研究生赵鑫智为论文第一作者。星空在线,星空在线(中国)张成杰教授、中国科学技术大学量子信息重点实验室许金时教授和李传锋教授为论文共同通讯作者。星空在线,星空在线(中国)为第一单位。

厄米算符的不确定性关系已通过多次实验得到证实。然而，以往的实验只测试了非厄米算符的特殊情况，即幺正算符的不确定性关系。对于非幺正算符的一般性非厄米算符的不确定性关系，目前还缺乏实验结果。为此本篇的工作研究了一般性非厄米算符的不确定性关系。这些算符通常具有复杂的特征值，难以通过实验直接测量。因此，需要在实验中设计一种非厄米算符的测量方法。在本文中考虑了单量子比特状态的实非厄米算符和复非厄米算符，并推导了这些非厄米算符的不确定性关系。本文通过损失一些光子在实验上实现了非厄米算符作用，并利用宣布式单光子源和Sagnac环形干涉仪实验验证了不确定性关系。

图1 实验装置图. 在两种情况（实数和复数）下测试两个非厄米算符A和B之间不确定关系的实验装置。图左下部分展示了实验中用到的宣布式单光子源。在实验上采用“大干涉环嵌套小干涉环”的方法来实现非厄密算符不确定关系的验证，非厄密操作的实现则通过“小干涉环”丢失一部分光子实现。图中（a）和（b）分别表示实数和复数情况下的非厄密操作。

本篇文章的实验适用于许多领域。首先，利用非厄米算符的不确定性关系，可以推导出任意参数无关非厄米哈密顿量的量子Cramr-Rao下界。其次，在任意维度上，利用非厄米不确定性关系可以度量量子信道下量子态的保真度。最后，非厄米算符的不确定性关系也可以应用于量子纠缠检测。这些非厄米算符不确定性关系的应用都可以通过实验实现。

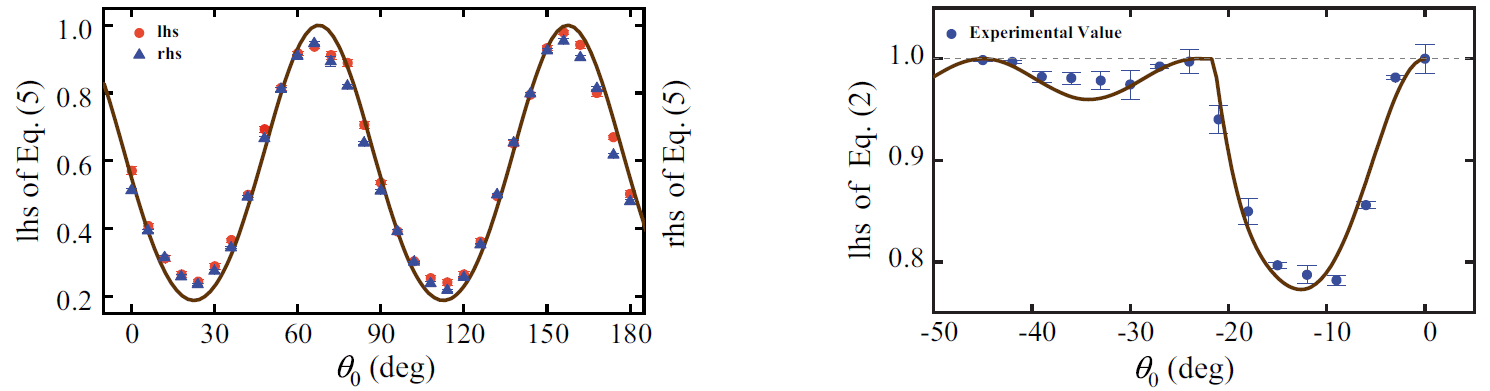
图2 实验结果图. 左图: 非厄米算符A和B都是实数，不同初态下不确定关系的实验点和相对应的理论曲线。右图: 非厄米算符A和B都是复数，不同初态下不确定关系的实验点和相对应的理论曲线。

该研究成果得到合肥国家实验室科技创新2030-“量子通信与量子计算机”重大项目（2021ZD0301200, 2021ZD0301400）、国家自然科学基金（11734015, 11821404，11875172）、宁波大学王宽诚基金等的支持。

论文链接：https://doi.org/10.1103/PhysRevLett.132.070203